ASSALAMUALAIKUM Wr, Wb
Welcome to blog Vektor Squarepants , yup seperti namanya blog ini akan membahas mengenai vektor. Mungkin teman-teman ada yang sudah mengetahui apa itu vektor dan mungkin ada yang tidak tahu, untuk mengetahui lebih jelas mengenai vektor mari kita simak penjelasan berikut ini:
A. Definisi Vektor dan Operasinya
1. Definisi Vektor
Vektor adalah suatu besaran yang mempunyai besar (panjang) dan arah. Besar (panjang) vektor digambarkan sebagai panjang ruas garis ( →). Vektor mempunyai titik pangkal dan titik ujung atau terminal, seperti pada gambar berikut:

Suatu vektor ditulis dengan huruf kecil dengan tanda panah di atasnya ataupun tanda panah di bawahnya, seperti :
Dan juga dapat ditulis dengan huruf kecil dicetak tebal, seperti a, b, dan c.
Untuk mendapatkan nilai suatu vektor dapat dicari dengan cara vektor kolom atau bentuk matriks , yang bentuknya seperti berikut :
Gambar 5.4 (a) Gambar 5.4 (b)
Pada Gambar 5.4 (a) , vektor AB dinyatakan dengan menyebutkan panjang dari A ke C dilanjutkan panjang C ke B. Panjang A ke C adalah 4 satuan dengan arah ke kanan, berarti merupakan komponen x dengan tanda positif. Adapun C ke B adalah 3 satuan dengan arah ke atas, berarti merupakan komponen y dengan tanda positif. Dengan demikian, apabila ditulis dalam bentuk matriks akan tampak sebagai berikut.
Dari Gambar 5.4 (b), kita dapat menyatakan vektor AB dengan cara menyebutkan panjang dari A ke D, kemudian dilanjutkan panjang D ke B. karena dari A ke D melangkah 3 satuan ke atas, berarti merupakan komponen y dengan tanda positif, sedangkan dari D ke B melangkah 4 satuan ke kanan, berarti merupakan komponen x dengan tanda positif. Dengan demikian, jika dinyatakan dalam bentuk matriks akan tampak sebagai berikut:
Penyajian ini dinamakan penyajian vektor dalam bentuk vektor matriks kolom atau sering disebut dengan vektor kolom.
 2. Operasi Aljabar pada Vektor
2. Operasi Aljabar pada Vektora. Penjumlahan Vektor
Tentukan vektor-vektor berikut dalam bentuk matriks!
a. vektor ae
b. vektor ab + bc + cd + de
penyelesaian:
Secara geometris penjumlahan vektor dapat dilakukan dengan dua cara yaitu dengan aturan segitiga dan aturan jajargenjang.
1a. Aturan Segitiga
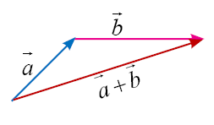 Seperti namanya, ketiga vektor dalam penjumlahan vektor dengan aturan
segitiga membentuk sebuah bentuk segitiga. Pada penjumlahan vektor
dengan aturan segitiga melibatkan tiga vektor. Vektor pertama adalah
Seperti namanya, ketiga vektor dalam penjumlahan vektor dengan aturan
segitiga membentuk sebuah bentuk segitiga. Pada penjumlahan vektor
dengan aturan segitiga melibatkan tiga vektor. Vektor pertama adalah 1b. Aturan Jajargenjang
 Seperti halnya penjumlahan vektor dengan aturan segitiga, penjumlahan
dua vektor dengan aturan jajar genjang juga melibatkan tiga vektor,
yaitu vektor pertama
Seperti halnya penjumlahan vektor dengan aturan segitiga, penjumlahan
dua vektor dengan aturan jajar genjang juga melibatkan tiga vektor,
yaitu vektor pertama b. Pengurangan Vektor
Gambar 5.13
Seperti yang telah kalian ketahui, jika arah suatu vektor berlawanan dengan arah vektor semula, misalnya vektor a , asalkan besarnya sama, dapat dituliskan dengan -a. Vektor - a disebut sebagai lawan vektor a.
Perhatikan gambar di samping, misalkan vektor b adalah lawan vektor a maka vektor b memiliki besar yang sama dengan vektor a, ditulis |a|= |b|. Akan tetapi, vektor b memiliki arah yang berlawanan dengan vektor a. Dalam hal ini, vektor b dapat dituliskan dengan b = -a.
Dari gambar di kanan, tampak bahwa vektor c-d = c + (-d)
c. Perkalian Vektor dengan Skalar
Yang dimaksud perkalian vektor dengan skalar ialah vektor tersebut dikalikan dengan skalar (bilangan real) .
Misalkan vektor b adalah vektor yang searah dengan vektor a , tetapi memiliki panjang(besar) 3 kali panjang vektor a. Vektor b dapat dituliskan dengan b = 3a. Apabila vektor b memiliki arah yang berlawanan dengan a dan panjang b adalah 3 kali panjang vektor a maka b dapat dituliskan b = -3a.
Secara umum, misalkan vektor a adalah suatu vektor dan m adalah bilangan real (skalar). Perkalian vektor a dengan bilangan real m adalah sebuah vektor b dengan
b = ma
Panjang b adalah |m| kali panjang vektor a. Apabila m<0 , vektor b berlawanan arah dengan vektor a , sedangkan apabila m>0, vektor b searah dengan vektor a. Notasi |m| berarti nilai mutlak m.
okehhhh, sampai jumpa di Blog selanjutnya....^_^












👍
BalasHapus👍
BalasHapus:v
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusTerima kasih ilmunya skarang sy tau materi tntng vektor👍👍
BalasHapus