Assalamualaikum, Wr.Wb.
Selamat datang kembali di vektor squarepants, ini adalah postingan blog kami yang ke-2 mengenai vektor. Kami harap blog kami ini bisa menambah ilmu teman-teman sekalian. Okeh kami langsung saja, di blog ini kami akan membahas vektor pada bidang atau dimensi dua. Mari kita simak penjelasan berikut ini:
1. Vektor Posisi
Vektor posisi suatu titik adalah sebuah vektor yang pangkalnya di titik pangkal koordinat dan ujungnya di titik itu. Agar lebih jelas perhatikan gambar berikut ini:
Berdasarkan gambar di atas manakah yang disebut vektor posisi? Vektor AB, OP, atau CD ? Yang termasuk vektor posisi adalah vektor OP merupakan vektor posisi dari titik P karena pangkalnya di titik pangkal koordinat O ( O,O) dan ujungnya di titik P.
Secara umum vektor posisi sebuah titik P (x,y) adalah
Dalam sebuah bidang ( dimensi dua) vektor satuan searah sumbu X dinamai i dan satuan searah sumbu Y dinamai j. Setiap vektor dapat dinyatakan sebagai vektor posisi ai + bj. Oleh karena itu, vektor posisi titik P ( 4,2) dapat ditulis dalam bentuk vektor p = vektor OP = 4 i + 2 j.
Secara umum vektor posisi dapat dinyatakan sebagai berikut :
2. Menyatakan Vektor Pada Bidang
Ketika membahas vektor posisi, kita telah memahami bahwa setiap vektor r dalam bidang dapat dinyatakan sebagai kombinasi linear vektor i dan j atau r = xi + yj , dengan (x,y) adalah koordinat titik ujung dari r .
3. Sifat-sifat Aljabar Vektor Pada Bidang
Jika m dan n bilangan real (skalar), kalian akan menemukan sifat-sifat berikut:
4. Panjang Vektor Pada Bidang
Dalam mencari panjang pada vektor yang digunakan adalah teorema (dalil) Pythagoras, yaitu:
5. Vektor Satuan Pada Bidang
Vektor satuan adalah suatu vektor yang ternormalisasi, yang berarti panjangnya bernilai 1.Umumnya dituliskan menggunakan tanda topi. Berdasarkan pengertian di atas berlaku hubungan:
6. Perkalian Skalar Dua Vektor pada Bidang
Misalkan diberikan dua vektor, yaitu vektor a dan b yang membentuk sudut 0 seperti gambar di samping. Perkalian skalar (dot product) dari vektor a dan b, dinotasikan dengan a.b.
Dan didefinisikan sebagai berikut:
C. Vektor Dalam Ruang (Dimensi Tiga)
1. Menyatakan Vektor dalam Ruang
Misalkan i,j, dan k masing-masing adalah vektor satuan dalam sumbu X,Y, dan Z. Diberikan titik P (3,4,1) pada sistem koordinat tersebut, sebagaimana gambar di atas.
Dengan menggunakan aturan penjumlahan vektor op dapat dinyatakan sebagai penjumlahan lebih dari satu vektor, yaitu:
op = oq + or + os = 3i + 4j + (1)k = 3i +4j +k
Secara umum, suatu vektor dalam ruang dapat dinyatakan sebagai kombinasi linear vektor-vektor satuan i , j, dan k. Misalkan a adalah sembarang vektor dalam ruang. Vektor a dapat dinyatakan sebagai vektor a = xi +yj + zk , dengan x,y,dan z adalah bilangan real. Vektor a juga dapat dinyatakan sebagai vektor baris atau vektor kolom.
2. Sifat-sifat Aljabar Vektor dalam Ruang
3. Panjang Vektor dalam Ruang
Seperti halnya kalian menentukan panjang vektor pada bidang, panjang vektor dalam ruang juga dapat ditentukan dengan cara yang sama. Misalkan diberikan vektor r = xi + yj + zk . Dengan memakai dalil Pythagoras, panjang vektor ini dapat ditentukan dengan rumus:
1. Menyatakan Vektor dalam Ruang
Dengan menggunakan aturan penjumlahan vektor op dapat dinyatakan sebagai penjumlahan lebih dari satu vektor, yaitu:
op = oq + or + os = 3i + 4j + (1)k = 3i +4j +k
Secara umum, suatu vektor dalam ruang dapat dinyatakan sebagai kombinasi linear vektor-vektor satuan i , j, dan k. Misalkan a adalah sembarang vektor dalam ruang. Vektor a dapat dinyatakan sebagai vektor a = xi +yj + zk , dengan x,y,dan z adalah bilangan real. Vektor a juga dapat dinyatakan sebagai vektor baris atau vektor kolom.
2. Sifat-sifat Aljabar Vektor dalam Ruang
3. Panjang Vektor dalam Ruang
Seperti halnya kalian menentukan panjang vektor pada bidang, panjang vektor dalam ruang juga dapat ditentukan dengan cara yang sama. Misalkan diberikan vektor r = xi + yj + zk . Dengan memakai dalil Pythagoras, panjang vektor ini dapat ditentukan dengan rumus:
CONTOH SOAL:
4. Vektor Satuan dalam Ruang
Misalkan diberikan sembarang vektor dalam ruang a = (x,y,z). Vektor satuan yang searah dengan vektor a , adalah a yang dapat ditentukan dengan cara yang sama dalam menentukan vektor satuan pada bidang, yaitu:
5. Perkalian Skalar Dua Vektor
Perkalian skalar dua vektor dalam ruang, konsepnya sama dengan perkalian skalar dua vektor pada bidang, yaitu:
dengan a dan b adalah vektor dalam ruang dan 0 adalah sudut di antara kedua vektor.
6. Hasil Kali Vektor atau Perkalian Silang (Pengayaan)
Perkalian vektor adalah perkalian antara vektor a dan vektor b yang menghasilkan vektor baru, misal c. Vektor baru hasil perkalian tersebut mempunyai besar |a||b| sin 0 dan arahnya tegak lurus terhadap vektor a dan vektor b.







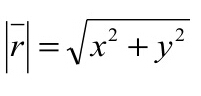












Tidak ada komentar:
Posting Komentar