Vektor

Sabtu, 06 April 2019

Perbandingan Ruas Garis dalam Bentuk Vektor

Assalamualaikum, Wr,Wb

Kali ini Vektor Squarepants akan memposting materi mengenai Perbandingan Ruas Garis dalam Bentuk Vektor, inilah materinya.....

D. Perbandingan Ruas Garis dalam Bentuk Vektor

Pada pembahasan sebelumnya, kalian telah mengetahui jika P, Q, dan R adalah titik-titik sembarang dalam sistem koordinat Cartesius maka vektor OP , OQ , dan vektor QR dapat diwakili oleh vektor-vektor p , q , dan r disebut vektor posisi dari titik-titik P , Q, dan R.

1. Perbandingan Segmen Garis

Perbandingan segmen garis pada Gambar 5.38 (a) dinamakan perbandingan di dalam, sedangkan perbandingan segmen garis pada Gambar 5.38 (b) dan Gambar 5.38 (c) adalah perbandingan di luar.

Sekarang perhatikan gambar berikut

Pada gambar di atas, diketahui vektor posisi titik P dan Q berturut-turut adalah vektor P dan vektor Q . Titik R pada ruas garis PQ mempunyai perbandingan m:n atau PR : RQ = m:n. Jika vektor posisi titik R adalah r, untuk menentukan vektor r dapat dilakukan dengan cara berikut:

Jadi berdasarkan penjelasan di samping vektor r dapat ditentukan menggunakan rumus:

2. Titik-titik Segaris (kolinear)

Suatu titik dikatatakan segaris (kolinear) adalah jika titik tersebut sama-sama melalui satu garis.

3. Teorema Ceva (Pengayaan)

Misalkan diberikan segitiga ABC . Titik D,E,F berturut-turut terletak pada sisi BC, AC,AB . Sedemikian rupa sehingga ruas garis AD,BE,CF berpotongan di satu titik maka berlaku teorema Ceva berikut:

E. Proyeksi Ortogonal Suatu Vektor pada Vektor Lain

Proyeksi merupakan cara pandang benda dari titik, garis,bidang yang merupakan suatu gambar yang akan kita lihat dari setiap sisi-sisinya.

Objek pada proyeksi skalar vektor ortogonal adalah panjang proyeksi vektor. Sedangkan pada proyeksi vektor ortogonal yang menjadi objek utamanya adalah vektornya. Vektor hasil proyeksi dapat ditentukan melalui rumus berikut.

Proyeksi vektor ortogonal $\vec{a}$ pada $\vec{b}$ .

$\vec{c} = \frac{\vec{a} \cdot \vec{b} }{\left| \vec{b} \right| ^{2} } \cdot \vec{b}$

Bagaimana menentukan panjang proyeksi ortogonal vektor a pada vektor b ?
Panjang proyeksi ortogonal vektor a pada vektor b adalah sebagai berikut:

Proyeksi vektor ortogonal $\vec{b}$ pada $\vec{a}$ .

$\vec{c} = \frac{\vec{a} \cdot \vec{b} }{\left| \vec{a} \right| ^{2} } \cdot \vec{a}$

Rabu, 23 Januari 2019

Vektor pada Bidang dan Ruang (Dimensi dua dan tiga)

Bismillahhirahmanirahim

Assalamualaikum, Wr.Wb.

Selamat datang kembali di vektor squarepants, ini adalah postingan blog kami yang ke-2 mengenai vektor. Kami harap blog kami ini bisa menambah ilmu teman-teman sekalian. Okeh kami langsung saja, di blog ini kami akan membahas vektor pada bidang atau dimensi dua. Mari kita simak penjelasan berikut ini:

1. Vektor Posisi
Vektor posisi suatu titik adalah sebuah vektor yang pangkalnya di titik pangkal koordinat dan ujungnya di titik itu. Agar lebih jelas perhatikan gambar berikut ini:

Berdasarkan gambar di atas manakah yang disebut vektor posisi? Vektor AB, OP, atau CD ? Yang termasuk vektor posisi adalah vektor OP merupakan vektor posisi dari titik P karena pangkalnya di titik pangkal koordinat O ( O,O) dan ujungnya di titik P.

Secara umum vektor posisi sebuah titik P (x,y) adalah

Dalam sebuah bidang ( dimensi dua) vektor satuan searah sumbu X dinamai i dan satuan searah sumbu Y dinamai j. Setiap vektor dapat dinyatakan sebagai vektor posisi ai + bj. Oleh karena itu, vektor posisi titik P ( 4,2) dapat ditulis dalam bentuk vektor p = vektor OP = 4 i + 2 j.

Secara umum vektor posisi dapat dinyatakan sebagai berikut :

2. Menyatakan Vektor Pada Bidang

Dari gambar di atas, tampak vektor op =4i dan vektor oq = 3j. Berdasarkan aturan penjumlahan, diperoleh sebagai berikut:

Ketika membahas vektor posisi, kita telah memahami bahwa setiap vektor r dalam bidang dapat dinyatakan sebagai kombinasi linear vektor i dan j atau r = xi + yj , dengan (x,y) adalah koordinat titik ujung dari r .

3. Sifat-sifat Aljabar Vektor Pada Bidang
Jika m dan n bilangan real (skalar), kalian akan menemukan sifat-sifat berikut:

4. Panjang Vektor Pada Bidang

Dalam mencari panjang pada vektor yang digunakan adalah teorema (dalil) Pythagoras, yaitu:

5. Vektor Satuan Pada Bidang

Vektor satuan adalah suatu vektor yang ternormalisasi, yang berarti panjangnya bernilai 1.Umumnya dituliskan menggunakan tanda topi. Berdasarkan pengertian di atas berlaku hubungan:

6. Perkalian Skalar Dua Vektor pada Bidang

Misalkan diberikan dua vektor, yaitu vektor a dan b yang membentuk sudut 0 seperti gambar di samping. Perkalian skalar (dot product) dari vektor a dan b, dinotasikan dengan a.b.

Dan didefinisikan sebagai berikut:

C. Vektor Dalam Ruang (Dimensi Tiga)
1. Menyatakan Vektor dalam Ruang

Misalkan i,j, dan k masing-masing adalah vektor satuan dalam sumbu X,Y, dan Z. Diberikan titik P (3,4,1) pada sistem koordinat tersebut, sebagaimana gambar di atas.
Dengan menggunakan aturan penjumlahan vektor op dapat dinyatakan sebagai penjumlahan lebih dari satu vektor, yaitu:
op = oq + or + os = 3i + 4j + (1)k = 3i +4j +k

Secara umum, suatu vektor dalam ruang dapat dinyatakan sebagai kombinasi linear vektor-vektor satuan i , j, dan k. Misalkan a adalah sembarang vektor dalam ruang. Vektor a dapat dinyatakan sebagai vektor a = xi +yj + zk , dengan x,y,dan z adalah bilangan real. Vektor a juga dapat dinyatakan sebagai vektor baris atau vektor kolom.

2. Sifat-sifat Aljabar Vektor dalam Ruang

3. Panjang Vektor dalam Ruang
Seperti halnya kalian menentukan panjang vektor pada bidang, panjang vektor dalam ruang juga dapat ditentukan dengan cara yang sama. Misalkan diberikan vektor r = xi + yj + zk . Dengan memakai dalil Pythagoras, panjang vektor ini dapat ditentukan dengan rumus:

CONTOH SOAL:

4. Vektor Satuan dalam Ruang

Misalkan diberikan sembarang vektor dalam ruang a = (x,y,z). Vektor satuan yang searah dengan vektor a , adalah a yang dapat ditentukan dengan cara yang sama dalam menentukan vektor satuan pada bidang, yaitu:

5. Perkalian Skalar Dua Vektor

Perkalian skalar dua vektor dalam ruang, konsepnya sama dengan perkalian skalar dua vektor pada bidang, yaitu:

dengan a dan b adalah vektor dalam ruang dan 0 adalah sudut di antara kedua vektor.

6. Hasil Kali Vektor atau Perkalian Silang (Pengayaan)

Perkalian vektor adalah perkalian antara vektor a dan vektor b yang menghasilkan vektor baru, misal c. Vektor baru hasil perkalian tersebut mempunyai besar |a||b| sin 0 dan arahnya tegak lurus terhadap vektor a dan vektor b.

Rabu, 16 Januari 2019

VEKTOR

BISMILLAHIRAHMANIRAHIM

ASSALAMUALAIKUM Wr, Wb

Welcome to blog Vektor Squarepants , yup seperti namanya blog ini akan membahas mengenai vektor. Mungkin teman-teman ada yang sudah mengetahui apa itu vektor dan mungkin ada yang tidak tahu, untuk mengetahui lebih jelas mengenai vektor mari kita simak penjelasan berikut ini:

A. Definisi Vektor dan Operasinya
1. Definisi Vektor
Vektor adalah suatu besaran yang mempunyai besar (panjang) dan arah. Besar (panjang) vektor digambarkan sebagai panjang ruas garis ( →). Vektor mempunyai titik pangkal dan titik ujung atau terminal, seperti pada gambar berikut:

Suatu vektor ditulis dengan huruf kecil dengan tanda panah di atasnya ataupun tanda panah di bawahnya, seperti :

Dan juga dapat ditulis dengan huruf kecil dicetak tebal, seperti a, b, dan c.

Untuk mendapatkan nilai suatu vektor dapat dicari dengan cara vektor kolom atau bentuk matriks , yang bentuknya seperti berikut :

Gambar 5.4 (a) Gambar 5.4 (b)

Pada Gambar 5.4 (a) , vektor AB dinyatakan dengan menyebutkan panjang dari A ke C dilanjutkan panjang C ke B. Panjang A ke C adalah 4 satuan dengan arah ke kanan, berarti merupakan komponen x dengan tanda positif. Adapun C ke B adalah 3 satuan dengan arah ke atas, berarti merupakan komponen y dengan tanda positif. Dengan demikian, apabila ditulis dalam bentuk matriks akan tampak sebagai berikut.

Dari Gambar 5.4 (b), kita dapat menyatakan vektor AB dengan cara menyebutkan panjang dari A ke D, kemudian dilanjutkan panjang D ke B. karena dari A ke D melangkah 3 satuan ke atas, berarti merupakan komponen y dengan tanda positif, sedangkan dari D ke B melangkah 4 satuan ke kanan, berarti merupakan komponen x dengan tanda positif. Dengan demikian, jika dinyatakan dalam bentuk matriks akan tampak sebagai berikut:

Penyajian ini dinamakan penyajian vektor dalam bentuk vektor matriks kolom atau sering disebut dengan vektor kolom.

2. Operasi Aljabar pada Vektor
a. Penjumlahan Vektor

Tentukan vektor-vektor berikut dalam bentuk matriks!
a. vektor ae
b. vektor ab + bc + cd + de
penyelesaian:

Secara geometris penjumlahan vektor dapat dilakukan dengan dua cara yaitu dengan aturan segitiga dan aturan jajargenjang.
1a. Aturan Segitiga
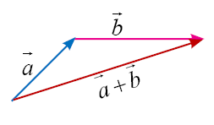Penjumlahan Dua Vektor Metode Segitiga

Seperti namanya, ketiga vektor dalam penjumlahan vektor dengan aturan segitiga membentuk sebuah bentuk segitiga. Pada penjumlahan vektor dengan aturan segitiga melibatkan tiga vektor. Vektor pertama adalah $\vec{a}$ , vektor ke dua adalah $\vec{b}$ , dan vektor ke tiga merupakan resultan kedua vektor (penjumlahan kedua vektor $\vec{a}$ dan $\vec{b}$ ).

1b. Aturan Jajargenjang
Penjumlahan Vektor Dua Vektor Aturan Jajargenjang

Penjumlahan Vektor Dua Vektor Aturan Jajargenjang

Seperti halnya penjumlahan vektor dengan aturan segitiga, penjumlahan dua vektor dengan aturan jajar genjang juga melibatkan tiga vektor, yaitu vektor pertama $\vec{a}$ , vektor ke dua $\vec{b}$ , dan resultan dari kedua vektor $\vec{a+b}$ . Jika pada penjumlahan vektor dengan aturan segitiga membentuk bangun segitiga, maka tidak begitu dengan penjumlahan vektor dengan aturan jajargenjang. Ketiga vektor pada penjumlahan vektor dengan aturan jajargenjang akan membentuk bangun jajargenjang jika ujung-ujung ketiga vektor dihubungkan dengan garis bantu.

b. Pengurangan Vektor

Gambar 5.13

Seperti yang telah kalian ketahui, jika arah suatu vektor berlawanan dengan arah vektor semula, misalnya vektor a , asalkan besarnya sama, dapat dituliskan dengan -a. Vektor - a disebut sebagai lawan vektor a.

Perhatikan gambar di samping, misalkan vektor b adalah lawan vektor a maka vektor b memiliki besar yang sama dengan vektor a, ditulis |a|= |b|. Akan tetapi, vektor b memiliki arah yang berlawanan dengan vektor a. Dalam hal ini, vektor b dapat dituliskan dengan b = -a.

Dari gambar di kanan, tampak bahwa vektor c-d = c + (-d)

c. Perkalian Vektor dengan Skalar
Yang dimaksud perkalian vektor dengan skalar ialah vektor tersebut dikalikan dengan skalar (bilangan real) .

Misalkan vektor b adalah vektor yang searah dengan vektor a , tetapi memiliki panjang(besar) 3 kali panjang vektor a. Vektor b dapat dituliskan dengan b = 3a. Apabila vektor b memiliki arah yang berlawanan dengan a dan panjang b adalah 3 kali panjang vektor a maka b dapat dituliskan b = -3a.

Secara umum, misalkan vektor a adalah suatu vektor dan m adalah bilangan real (skalar). Perkalian vektor a dengan bilangan real m adalah sebuah vektor b dengan

b = ma

Panjang b adalah |m| kali panjang vektor a. Apabila m<0 , vektor b berlawanan arah dengan vektor a , sedangkan apabila m>0, vektor b searah dengan vektor a. Notasi |m| berarti nilai mutlak m.

okehhhh, sampai jumpa di Blog selanjutnya....^_^

(\begin{matrix}  \end{matrix})